（2016年7月取材）

■部員数

13人(うち1年生4人・2年生4人・3年生5人)

■答えてくれた人

今智哉くん(3年)、石川真智くん(3年)　永崎遼太くん(3年)、井坂将隆くん(3年)

今年は二次元方向にメトロノームを配列して同期現象の出現を調べる

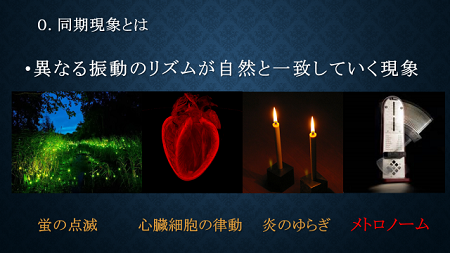
私たちは二次元方向でのメトロノームの同期現象について研究しました。同期現象とは、異なる振動のリズムを持っている物体同士が相互作用し自然と時間を経て同じリズムになることを指します。色々な所で見ることができますが、私たちはメトロノームという振動子でこの同期現象について実験しました。 

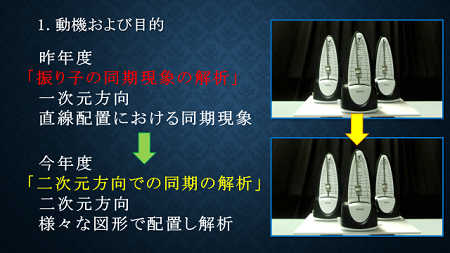
私たちは昨年度、一直線上に配置したメトロノームの同期現象について実験し、それが起こるために必要不可欠な条件が、自由に動ける台と、メトロノームのような強制振動子であることがわかりました。強制振動子とは、ゼンマイ仕掛けのメトロノームのように外部から力を加えて振動する振り子のことです。今年度は、二次元方向にメトロノームを設置した際の同期現象の解析を試みました。

同期現象が発生する時、台は回転運動をする…ということは？

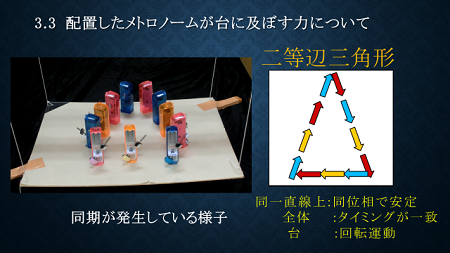
まずは、バラバラに振動するメトロノームが二次元的な配置をとった時、どのような挙動をするのか実験しました。左のスライドのように、四隅を垂直に糸でつなげて宙に浮かせます。

そして、どの方向にも平行移動できる台の上で、バラバラに振動しているメトロノームを下図のように4つの図形の形に配置しました。(正方形と正三角形は1辺30cm、円は半径10cm)

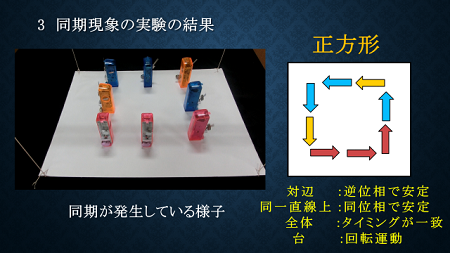
正方形配置にした場合の結果です。同じ辺のメトロノームは同位相（振動するタイミングが一緒）で、対辺同士のメトロノームは逆位相（振動するタイミングが逆）となりました。また台は回転運動をしていました。

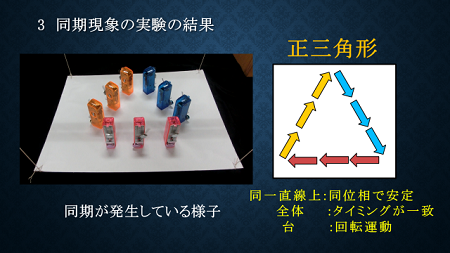
次に、正三角形配置の場合の結果です。同じ辺のメトロノームは同位相となりました。また、台は回転運動をしました。

次に円の接線方向に配置した場合の結果です。向かい合うメトロノームが逆位相となりました。台は回転運動をしました。

最後に、円の法線方向に配置した場合の結果です。全体的にタイミングは一致せず、同期現象は発生しませんでした。このとき台は一定の運動をしませんでした。

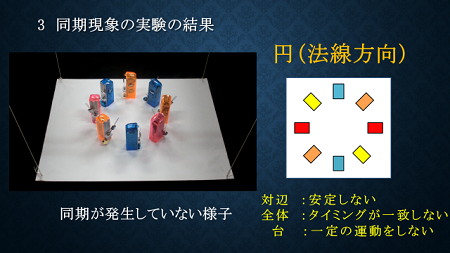
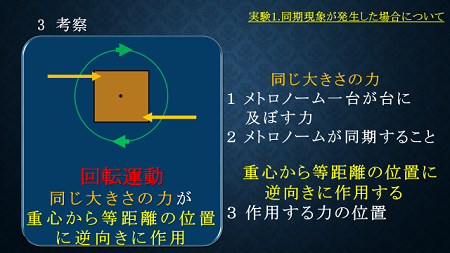
これらのことから、メトロノームが同期現象を示した時、台は回転運動のみしており、同じ大きさの力が重心から等距離に逆向きに作用していた、と考えました。

そこでまず、台全体に及ぶ力を知るために、メトロノーム1台が台に及ぼす力を計算しました。メトロノームの振り子は上下にそれぞれ一つずつおもりが付いている構造なので、それぞれの成分について振り子の軸方向に働く合力を求めました。これは、台に力を及ぼすのは軸方向の成分のみだからです。 

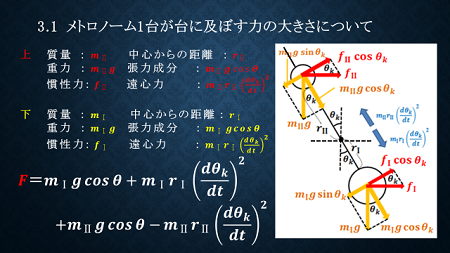
そして、その軸方向の合力のうち、台は水平方向にしか動かないので水平方向成分を求めました。

メトロノームの位相の一致をコンピュータシミュレーションで再現！

次にメトロノームの位相の一致をコンピュータシミュレーションによって再現させることを試みました。そこでメトロノームの針の角加速度について考えました。メトロノームは、(1)台の運動による慣性力、(2)ゼンマイの力、(3)抵抗力の3種類の外力を受けています。 

まず台の運動による慣性力ですが、先ほど算出した合力が各メトロノームから伝わるため、台は加速度を持った運動をします。しかし台を静止していると見なすと、台にかかる加速度とは逆向きの方向に見かけ上の力である慣性力がメトロノームの針にかかると見なせます。

次にゼンマイの力です。これは針の進行方向にかかる力で、振動の減衰に抵抗するために、ある一定の振れ角の時のみ働きます。私たちは、このようなゼンマイの力をモデル化しました（下図）。

3つ目の抵抗力については、時間に依らずに一定の摩擦が働くとして、下図のようにモデル化しました。

したがって、以上の3つの式を足し合わせたものをメトロノームの針にかかる合力とし、各メトロノームの針の振れ角度と時間に関する連立微分方程式が立ちました。ここでメトロノームを3つとして、コンピューターでシミュレーションさせてみました。

下のグラフは、横軸が時間、縦軸が各メトロノームの位相を表しています。

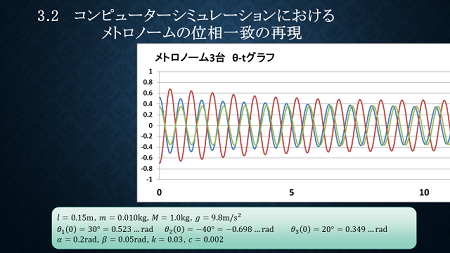
バラバラだった針の振幅は、下図のように同期しました。

配置したメトロノームは台にどのような力を及ぼすか

以上のメトロノームが台に及ぼす力の代数的解析と、メトロノームが同期することのシミュレーションの二点により、台には同じ大きさの力が働くことが裏付けられました。

次にそれらの力が重心から等距離の位置に作用することを確かめるために、メトロノームの配置について考察しました。

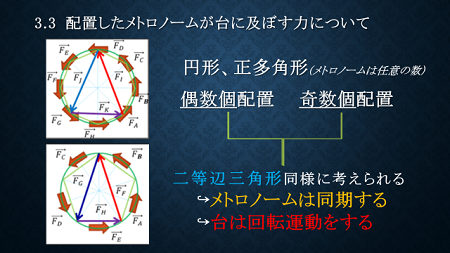
正方形、正三角形型に配置した場合について、図のようにそれぞれのベクトルを足し合わせるとゼロになることは明らかです。またトルク（回転しようとする力）が発生することも分かります。

次に円の接線方向に配置した場合です。この場合も、図のように合力ベクトルを考えるとトルクが発生することがわかります。

また合力ベクトルの形から、円形配置は二等辺三角形の配置と同様に考えられることが分かったので、二等辺三角形の配置で追加実験を行いました。すると二等辺三角形でも同期現象が確認できました。 

したがって任意の数のメトロノームを円形あるいは正多角形型に配置するとき、二等辺三角形型に配置した時と同様にトルクが発生し、メトロノームの同期現象が起こると考えました。

円の法線方向ではなぜ同期現象が発生しないのか

次に台が回転運動をしなかった場合についての考察です。円の法線方向にメトロノームを配置した時、台は回転運動に収束しませんでした。同期現象は、一定の運動に収束する台の影響を受けて発生するものなので、台の運動が収束しなかったため同期もしませんでした。これは、メトロノームの配置的に合力ベクトルが安定しなかったためと考えました。

実際にそれぞれの位相を考えてみると、円の法線方向に配置した時は、以下の5通りで安定した運動に収束するという仮説が立てられましたが、それぞれが発生過程で打ち消しあってしまい同期現象を観測することはできませんでした。 

メトロノームのテンポと同期現象が発生するまでの時間にはどんな関係があるのか

さらに、メトロノームのテンポと同期するまでの時間に関係性があるのか調べました。正方形配置にしたメトロノームを一定間隔で順番に針を倒し、同期現象に至るまでの時間を測定しました。 

結果、テンポが速いほど同期現象に至るまでの時間が早いことが判明しました。なお、テンポの単位はBPM（※）としました。

※Beat Per Minute :1分間の拍の数の単位。音楽の世界で一般的な単位を研究において使用しました。楽譜の左端に♪＝○と書いてあるのがそれです。♪＝100であればBPM100です。

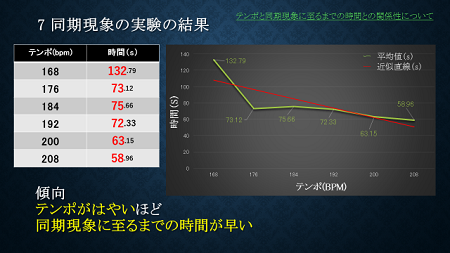
同期現象は個々のメトロノーム間の相互作用によって発生します。メトロノームのテンポが速ければ、台に与える力の周期も短くなります。つまり単位時間当たりに台に与える力の大きさも増えるので同期現象に早く到達すると考えられます。

今年はメトロノームの二次元方向の配置と同期現象の関係、同期現象に至るまでの時間とテンポの関係という切り口から昨年の研究を拡張することに成功しました。今後は、逆位相で安定する同期現象の解析や、メトロノーム以外での同期現象についての解析に挑戦してみたいと思います。

■研究を始めた理由・経緯は？

昨年度は、一次元方向を自由に動く、空き缶を用いた台の上での同期現象の解析によって、同期現象には、メトロノームの力が作用しあう媒体となる台と強制振動子（本研究ではメトロノーム）が必要であることがわかりました。私たちはこの研究でメトロノームの同期現象について興味を持ち、さらに調べてみたいと思いました。

そこで、今年度は、二次元方向を自由に動く、4本の糸で繋がれ、宙に浮いた台での同期現象によってメトロノームの配置と同期現象の関係を調べようと思いました。また、メトロノームのテンポの速さとリズムが揃うまでの時間の関係性について、なんとなくテンポが速いほど揃うというイメージを持っていましたが、それを裏付けるデータがなく、また、実際どの程度変化するのかわからなかったので、メトロノームのテンポの速さとリズムが揃うまでの時間の関係性について研究しました。

■今回の研究にかかった時間はどのくらい？

1週間に4時間で、1年間かけて研究しました(昨年度からの研究も合わせると2年間です)。

■今回の研究で苦労したことは？

まず、先輩たちの研究を理解するところから始まったのですが、これが大変でした。数学や物理の予習も行って理解できました。総試行回数100回以上を超える実験はもちろん苦労しましたが、もっと大変だったのは解析と考察です。解析については、数学が得意な永崎が家に持ち帰って頑張りました。また、同期現象が起きなかった円の接線に対する法線方向配置の考察は大変でした。完璧とは言えませんが、一つの結論にたどりつけてよかったです。あまりにも没頭しすぎて夜8時を過ぎてしまい、怒られたこともありました（笑）。

■「ココは工夫した!」「ココを見てほしい」という点は？

「昨年度の研究とは違う何かをしよう！」ということで研究を進めました。二次元方向でメトロノームの合力が台に及ぼす力の考察はその一つです。その時に、昨年度でも意識していた「高校で学ぶ知識で質の高い研究をしよう」という目標に基づいて、ベクトルを使って同期現象の解析をしました。また、研究発表ではあまり説明しませんでしたが、実は台の調整をかなり工夫しました。糸の利用という発想も、時間をかけて生まれたものです。この構造が、台の回転（実際にはメトロノームは往復するので台はひねって戻る動きをする）によるメトロノームの同期現象という新たな現象を生み出しました。

■今回の研究にあたって、参考にした本や先行研究

・「振り子の同期現象はなぜ起こるのか～非線形リズムの世界を探る～」茨城県立土浦第一高校(第39回全国高等学校総合文化祭自然科学部門)<みらいぶ＞

・「メトロノームの同期現象＋」宮崎大学工学部情報システム工学科 伊達章

■今回の研究は今後も続けていきますか？

私たちは夏で部活引退ですが、個人的にはまだまだ調べたいなということは山ほどあります。テンポが一定の速さより遅いとなぜ発生しなくなるのか、また、同期現象発生の条件の一般化（○○のときに発生する！と断言できる法則の発見）、また、逆位相でメトロノームが安定する条件などです。勉学面も忙しくなってきて大変でしょうが、後輩達には納得できる研究を作り上げてほしいです！

■ふだんの活動では何をしていますか？

物理実験部活動の柱は二つあります。一つは今回発表したような研究活動、もう一つは、物理の面白さを校内外に広めることです。そのために、土浦一高の文化祭「一高祭」、産総研の一般公開、「青少年のための科学の祭典日立大会」に参加しています。一見すると数式だらけで取っ付きにくそうですが、その一つひとつは実に簡潔なものであり、またこれまで発見された物理法則の中には驚きのものや美しいものがたくさんあります。私たちの活動が、誰かを科学や物理の美しい世界へといざなうきっかけとなれば幸いです。

■総文祭に参加して

他校の皆様の研究発表を見たときは、正直に言うと、びっくりしました。総文祭で発表された研究のクオリティはとても高かったです。全力を出し切ったとはいえ、表彰までは不安でした。この1年、昨年の総文祭での先輩たちのようになりたいと努力したことの集大成が、このように結果に表れたことは嬉しく思っています。細かい反省点はありますが、悔いはもうありません。この体験をこれからの人生に生かしていきたいです。

最後になりますが、スタッフとしてご協力していただいた広島県の高校生や先生の皆様、お疲れ様です。一昨年のいばらき総文で、私たちもスタッフとして関わりましたので、その大変さはよく分かります。スタッフの皆様のおかげで生徒交流会のクイズも楽しかったです。広島のレモンが水素イオンの問題になったときは、やられたと思いました（笑）。本当にお疲れ様でした。

※土浦第一高校の発表は、物理部門の優秀賞を受賞しました。

◆2016ひろしま総文の他の発表をみる ＜2016ひろしま総文のページへ＞