2016ひろしま総文 自然科学部門
コイルガンを使ってエネルギー変換効率の限界を見究める
【物理】佐賀県立佐賀西高校サイエンス部
(2016年7月取材)

■部員数
26人(うち1年生13人・2年生6人・3年生7人)
■答えてくれた人
小栁伊央くん(3年)
高性能なコイルガンを目指して
鉄芯の飛距離に注目して運動エネルギーを測定する

一般に、あるエネルギーを他の形のエネルギーに変換するときには熱などの形で一部のエネルギーが失われてしまいます。そこで変換前と変換後のエネルギー量の比を「エネルギー変換効率」と呼び、私たちの生活において重要な概念となっています。
今回、私たちはコイルガンという電気エネルギーを運動エネルギーに変換する装置を使って、この装置の変換効率の限界を目指そうとしました。
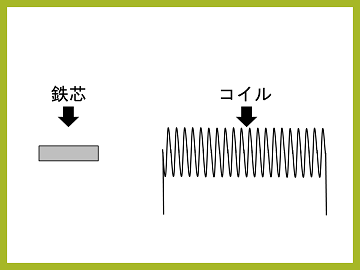
まずコイルガンの原理について説明します。コイルに電流を流すと、コイルは磁石のように振る舞います。ここで図のように鉄芯を並べると、鉄芯も棒磁石のように振る舞い、コイルに引き寄せられる方向に力が働きます。もちろんコイルは空洞ですので、鉄芯はコイルに当たることなく通過し、まるで銃(ガン)のように勢いよく発射されます。
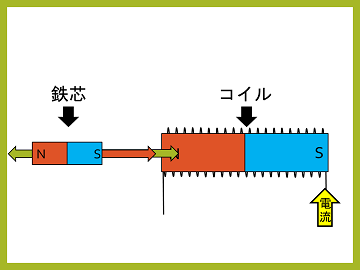
ここで注意しなければいけないのが、コイルに電流を流し続けると、鉄芯はコイル中心に向かって力が加わるため、コイル中心を超えると逆方向に力が加わり、元の位置に逆戻りします。そこで力の方向が変わる前に電流を止めることでコイルも鉄芯も磁力が無くなり、鉄芯は慣性で引き合う方向に進み続けます
実際にコイルガンが鉄芯を射出する動画をご覧ください。

ここで鉄芯は垂直方向には自由落下、水平方向には等速直線運動をしていることがわかります。運動エネルギーは1/2mv²(mは質量、vは速度)で与えられます。私たちの実験では、鉄芯の質量mを一定にしたので、運動エネルギーは鉄芯の初速度vのみに依ります。発射する台の高さも固定したので、床に落ちるまでの自由落下時間、すなわち飛行時間は一定となります。
水平方向の速度は距離÷時間で求めることができ、飛行時間が一定であるので、運動エネルギーの大きさを決める初速度vは鉄芯の飛距離のみに依存します。したがって主に鉄芯の飛距離に着目して4つの実験を行いました。
実験1 鉄芯の初期位置と飛距離の関係を調べる
最初の実験では、鉄芯の初期位置と飛距離の関係を調べました。具体的にはコイルの中心から鉄芯までの距離を0.25cm刻みで変えてそれぞれの飛距離を測定しました。実験条件は以下の通りです。
・19Vで1分充電
・コイルは3重巻きのものを使用
・コンデンサは計8000μF
・34cmの高さから射出
・2cmの鉄芯を用いた

誤差を極力排除するため、私たちはこの射出動作を合計700回行いました。結果をまとめたグラフがこちらです。
このグラフから、鉄芯がコイルの中心から2.25cm離れているときに飛距離が最高になることがわかりました。このときに、電流が流れている間に鉄芯がされた仕事が最大になっていると考えられます。
実験2 コイルの巻き数と飛距離の関係を調べる

実験2では、コイルの巻き数と飛距離の関係について調べました。ここでいう巻き数とはコイルの芯に使っているストローに対して隙間なく巻くことを1重巻き、その上にさらに隙間なく巻くことを2重巻き、と定義します。そして1重から5重巻きまで巻き数を変えたコイルを使って飛距離を測定しました。実験条件は先ほどの実験1と同じですが、鉄芯の初期位置は先ほどの実験で最も飛距離が長かった2.25cmとしました。結果をグラフにまとめたのがこちらです。
1,2重巻きでは射出できなかったのに対し、3,4,5重巻きでは飛距離に差が出ませんでした。巻き数が小さいと射出されなかったことから、巻き数を加えることで鉄芯に加わる力は大きくなっていることがわかります。しかし、それ以上の巻き数を加えても飛距離に差がでなかったのは、引力が大きくなるとともに斥力も大きくなったからではないかと考えました。
実験3 巻数と初期位置を両方変えてみる
実験3では、実験1と2の複合実験をしました。異なる巻き数のコイルに対してそれぞれ鉄芯の位置を0.25cm刻みに変えて飛距離を測定しました。下図が結果をまとめたグラフです。
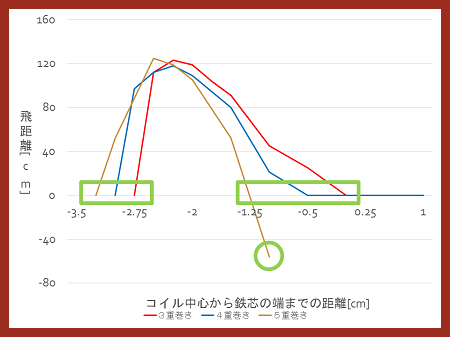
まずそれぞれの折れ線グラフがゼロと交わる位置に着目します。巻き数が増えるにつれて射出される位置の限界は伸びています。ここからも巻き数が増えるにつれて鉄芯に加わる引力は強まると考えられます。
次にグラフ下部の1.25cmあたりの部分を見ると5重巻きの時、飛距離はマイナスになっています。これは逆方向に射出されたということです。実験2では巻き数が増えれば斥力も増えるのではないかと考察しましたが、この実験によって鉄芯がされた仕事の合計が負になっている事例も確認できました。
実験4 鉄芯に加わる引力の推移を調べる
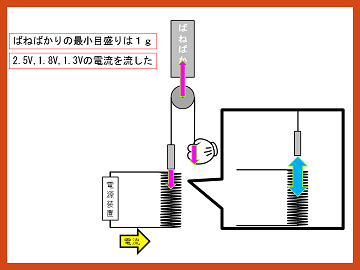
また鉄芯にどのような力が加わっているのかを調べるために、図の実験を行いました。鉄芯に糸を通し、ばねばかりにつないで、手で持ちます。鉄芯の下には、電源装置につないだコイルを置きました。
まずコイルに電流を流すと、鉄芯とコイルの間に引力が働きます。ここで鉄芯が動こうとする力を手で押さえて静止させます。すると、ばねばかりには釣り合う二つの力、すなわちコイルガンの引力と手が引っ張る力が加わります。したがってコイルガンの引力の二倍の力が測定できます。このことから、ばねばかりの最小目盛りである1gの半分である0.5g単位での測定が可能となりました。

今回は、従来の実験条件に加えて三つの電圧を使って鉄芯とコイルの中心からの位置と加わる力の関係を調べました。結果をグラフにまとめたのがこちらのグラフです。
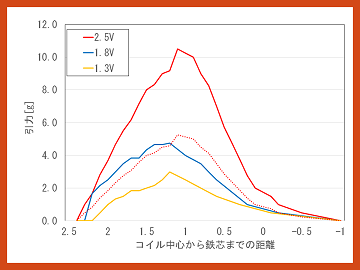
四捨五入しているのでわかりにくいですが、2.5Vの1/√2倍が1.8V、1/2倍が1.3Vです。下の図では、2.5Vのグラフを1/2倍したものを赤い点線で追加しました。

次に、2.5Vのグラフを1/4倍したものを点線で加えました。
すると2.5Vの1/√2倍の電圧を加えたコイルガンの引力は、それぞれの位置で大体1/2倍になっています。また、2.5Vの1/2倍の電圧を加えた引力は大体1/4倍になっていることがわかります。したがって、鉄芯に加わる引力はコイルに流れる電圧の2乗に比例すると考えました。また電力Pはオームの法則V=IRよりP=IV=V2/Rとなり、電力も電圧の2乗に比例しているので、鉄芯に加わる引力は電力に比例しているのではないかと考えました(ここでVは電圧、Iは電流、Rは抵抗を表しています)。
鉄芯に加わる力はコイルにかかる電圧の二乗に比例すること
まとめです。実験1より、鉄芯の初期位置と飛距離に関係があることがわかりました。また実験2,3から、巻き数を多くすることによって鉄芯に加わる力を大きくなることがわかりました。しかし電流を流す時間の都合上、巻き数が大きすぎると鉄芯が受ける仕事が負になると考えられました。また実験4から、鉄芯に加わる力はコイルにかかる電圧の二乗に比例することがわかりました。
今後は鉄芯の条件を変えたときの飛距離の変化や、コイルの巻き数を増やすことの限界を調べていきたいと思います。
■研究を始めた理由・経緯は?
コイルガンの前に、磁力を使って射出するガウス加速器の研究をしていたのですが、磁力(射出速度)に限界を感じたからです。
■今回の研究にかかった時間はどのくらい?
1日2時間程度で、2015年5月からです。
■今回の研究で苦労したことは?
単調な作業を繰り返し、得られた多数のデータの平均を取ることで、信頼できるデータを作ることです。
■「ココは工夫した!」「ココを見てほしい」という点は?
実験条件をできるだけ同じにするために、コイルの温度に注意を払いました。また、飛距離を正確に得るためにカメラを用いて測定しました。
■今回の研究にあたって、参考にした本や先行研究
特にありません。
■今回の研究は今後も続けていきますか?
射出する鉄芯やコイルの導線の材質を変えたときの変化を調べたいと考えています。
■ふだんの活動では何をしていますか?
中学校に出前実験授業に行っています。また、文化祭で展示をしたり、体育祭で部活動対抗リレーに出たり、佐賀県立宇宙科学館の春の企画展(ビーコロ制作)に参加したりしています。
■総文祭に参加して
今回の発表では反省すべき点も多く、また、他校の発表からも参考にできる点が多くありました。来年こそは入賞目指してがんばります。
◆2016ひろしま総文の他の発表をみる <2016ひろしま総文のページへ>
 みらいぶっくグループ
みらいぶっくグループ






