つくばサイエンスエッジ2018
丸にとらわれたお星さま!?ファンタジックで美しい数学
~星型正n角形k点飛ばしにおける面積の一般化公式を導く~【数学・情報・コンピュータ】
文京学院大学女子高校 代表者 高柳茜さん
(2018年3月取材)
きっかけ~爪に塗られた星のマニキュアを見てひらめいた!

星型正多角形のデザインで有名なものに、魔術的なデザインとして知られる「五芒星」があります。この星型五角形(五芒星)を含めた星型正n角形について、今回、まったく新しい視点で、面積の一般公式を導き出しました。
実は、手の爪に塗られた星のマニキュアを見て、爪の中に一体、どのぐらい大きな星型が描けるだろうかという疑問を抱いたのがきっかけです。円に内接する星の図をイメージし、そこから星型の面積の求め方に着目し、今回の研究を始めました。
星型多角形については、星型多角形の内角の和の公式は、すでに証明されていますが、面積の公式に関しては、まだ存在しません。その理由として、星型多角形には複合星型多角形など様々な種類の星型があることや、その星型という独特な形が面積の一般化を困難にしている原因でないかと考えました。そこで、まず左右対称性のある星型正多角形の面積を考えました。
誰も考えなかった! 星型正多角形のまったく新しい定義
星型正多角形の面積を一般化するために、独自に星型正多角形の定義を定めました。
半径rの円に内接する正n角形の頂点をk点として、そこから別のk点に線を「飛ばし」、結んでできる星型を「星型正n角形k点飛ばし」と定義しました。例えば、正八角形の頂点を1つずつ飛ばしながら結んでできる星型は「星型正八角形1点飛ばし」、2つずつ飛ばしながら結んでできる星型は「星型正八角形2点飛ばし」と呼びます。
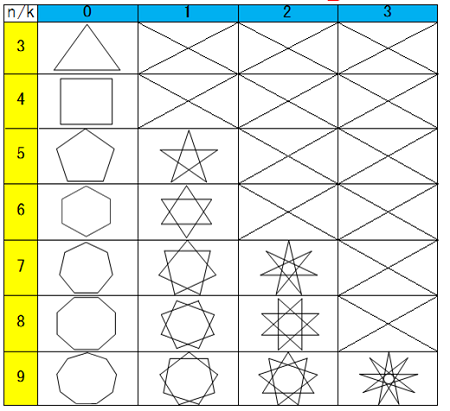
n=頂点の数(正n角形)
k=頂点の飛ばし方(k点飛ばし)
星型正n角形k点飛ばしの面積の一般化 ここがポイント!
星型正五角形の星型をよく見ると、合同な5個の四角形に分割できることわかります。さらにそれは10個の合同な三角形に分割できます。この合同な三角形の面積がわかれば、五芒星の面積が求めることができるのでないか。またその延長で、星型正n角形k点飛ばしの面積の一般化ができるだろうと考えました。そこが一番大きなポイントです。
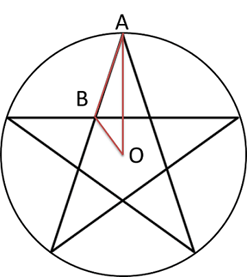
星型正n角形k点飛ばしの面積の証明!
星型の中の合同な三角形をAOBとします。星型の星の面積は、三角形AOBを10倍して、三角形の面積の公式に当てはめれば導き出せます。
三角形の面積Sを求める公式は、S=三角形の2辺×sin(2辺の交差する角)÷2です。三角形の2辺と、2辺に挟まれた内角がわかれば、三角形AOBの面積は導けます。
まず2辺に挟まれた内角は、円周角は円の中心角の半分であるという円周角の定理を使うと、中心角の半分の半分になることがわかりました。
次に2辺の長さですが、そのうち1辺AOは円の半径です。もう1辺ABの長さは、三角形AOBに正弦定理を用いると解けます。三角形の内角と対辺の関係から計算して、辺ABの長さを導き出しました。
このようにして2つの辺と、2つの辺が交差する内角のすべてわかりました。それを面積の公式に代入することで三角形AOBの面積もわかりました。さらにそれを10倍すると、五芒星(星型正五角形)の面積です。
同様の計算法を使って星型正n角形に一般化を試みたところ、いくつかの計算手順を踏んだ結果、次のように、星型正n角形1点飛ばしの面積を導くことができました。
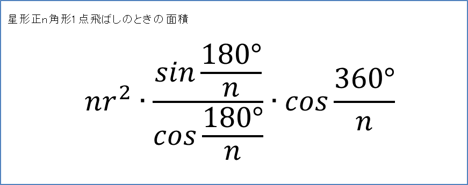
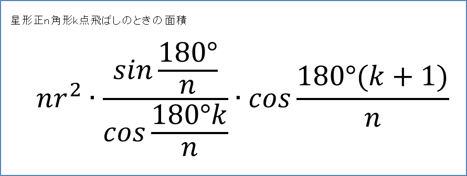
次に、同様の手順で3点、4点飛ばしと続けていき、最後に、以下のような星型n多角形k点飛ばしの面積の一般化を行うことができました。
今後の展望
~例えばヒトデ 複雑な星型多角形の面積を求めるソフトを作りたい!
今後は星型多角形の面積の一般化についても考察していきたいと考えています。ヒトデなどの生物に見られる星型多角形は複雑です。こうした星型正多角形に近い生物などの形を、画像解析によって認識させ、今回一般化した式で、より迅速かつ正確に面積を求めることができるソフトを作成したいと考えています。
講評の先生のコメント
~大人が思いもよらなかったファンタジックな数学研究!
――星型の五角形というのは、幾何学でわりあい一般的に使いますよね。それをきちんとn型でk点飛ばしというような条件を決めて一般化するというのは、ちょっと思いもよらなかったので、率直なところ大変びっくりしています。
 みらいぶっくグループ
みらいぶっくグループ






